Birim (Trigonometrik) çember [değiştir]
Merkezi orijin ve yarıçarpı 1 birim olan çembere birim çember veya trigonometrik çember denir. Birim çemberin denklemi
şeklindedir.
Birim çemberde verilen bir  noktası; noktası;
- 1.bölgede ise

- 2.bölgede ise

- 3.bölgede ise

- 4.bölgede ise
 dır. dır.
- Açıyı ölçmek demek, açının kolları arasındaki açıklığı belirlemek demektir.
Açı ölçü birimleri üç tanedir.
DERECE: Bir tam çember yayının 360 eş parçaya bölünmesiyle elde edilen her bir yayı gören merkez açının ölçüsüne 1 derece denir.
GRAD: Bir tam çember yayının 400 eşit parçaya bölünmesiyle elde edilen her bir yayı gören merkez açının ölçüsüne 1 grad denir.
RADYAN: Bir çemberde yarıçap uzunluğundaki yayı gören merkez açının ölçüsüne 1 radyan denir.Çember yayının ölçüsü 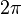 radyandır ve radyanla çarpılarak bulunur. radyandır ve radyanla çarpılarak bulunur.
Sarma fonksiyonu [değiştir]
Reel sayılar kümesinden birim çember üzerindeki noktalara tanımlanan fonksiyona sarma fonksiyonu denir.
Sarma fonksiyonunu s ile, birim çemberi de C ile gösterirsek;
 yazilabilir. yazilabilir.
 oldugunda oldugunda  olur. olur.
Bir açının esas ölçüsü [değiştir]
a) Verilen açı  ya da ya da 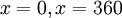 ise; ise;
 in esas ölçüsü kendisidir. in esas ölçüsü kendisidir.
b) Verilen açı  ya da ya da  ise; ise;
 in 360 a bölümünden kalan esas ölçüyü verir. in 360 a bölümünden kalan esas ölçüyü verir.
c) Verilen açı  ise; ise;
 360 a bölümünden kalan 360 a bölümünden kalan 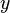 olsun. olsun.
O halde,  in esas ölçüsü in esas ölçüsü 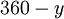 dır. dır.
Trigonometrik fonksiyonlar [değiştir]
olarak adlandırılır.
Bu tanımlardan görülebileceği gibi, bu fonksiyonlar arasında,

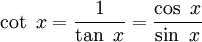


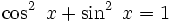 (Pisagor teoremi) (Pisagor teoremi)
ilişkileri vardır.
Dik üçgenlerde bazı açıların trigonometrik oranları [değiştir]
Trigonometrinin kullanım alanları [değiştir]
Trigonometri birçok fen biliminde, matematiğin diğer alanlarında ve çeşitli sanatlarda yaygın bir biçimde kullanılmaktadır. Trigonometriyi kullanan bazı dallar şunlardır:
jeofizik, kristalografi, ekonomi (özellikle de finansal pazarların analizinde), elektrik mühendisliği, elektronik, jeodezi, makine mühendisliği, meteoroloji, müzik kuramı, sayı kuramı (ve dolayısıyla kriptografi), oşinografi (okyanus bilimi), farmakoloji (eczacılık), optik, fonetik, olasılık kuramı, psikoloji, sismoloji...
Trigonometri yukarıda örneklendiği gibi birçok farklı alana farklı katkılarda bulunmuştur. Örneğin Pisagor kuramının isim babası PisagorFourier serileri sayesinde trigonometrik fonksiyonlar farklı fonksiyonları temsil etmekte kullanılırlar ve bu sayede trigonometri birçok farklı dalda kullanım olanağı bulmuştur. Böylece ısı akışı ve difüzyon başta olmak üzere özellikle periyodik özellik gösteren kavramların incelendiği birçok dalda ve fenomende trigonometrik fonksiyonlar kullanılabilmiştir; akustik, radyasyon ve elektronik gibi. matematiksel müzik kuramına ilk katkıda bulunan isimlerdendir. Oşinografide bazı dalgaların sinüs dalgalarına benzerliği ilgili incelemelerde trigonometrinin kullanımına olanak tanımıştır. Bunun dışında |